MULTIAXIAL
For multiaxial calculations, the winLIFE MULTIAXIAL module is required in addition to winLIFE BASIC.
From Component Loading to Local Stress/Strain
The knowledge of the local stress (stress, strain) is an essential prerequisite for a fatigue life calculation. There are different problems that need to be solved using different theoretical approaches. On the one hand, the type of component to be analysed (rigid, flexible, multi-body system) plays a role, and on the other hand, the type of load.
Loads can be specified as load-time curves (time series), as load spectra (frequency of load steps) or as spectral density of the load as a function of frequency (power density spectrum). When to use each of these methods is briefly explained here.
|
Component |
Load given as |
Solution method |
Interface macros / |
|
|
Load time history |
Superposition of standard FE loading conditions by corresponding scaling of the load time functions. |
FEMAP, ANSYS |
|
Load spectrum |
Superposition of standard FE loading conditions by corresponding scaling of the load time functions |
FEMAP, ANSYS |
|
|
|
Random Fatigue: |
Calculation possible but extensive preparatory work necessary by the user. |
|
|
Multi-body systems, partially elastic, large relative movements, inert forces |
Load time history is exciting the Multi-Body -System |
Transient Analysis: Importing the stress tensor-time function from the FEM/MKS calculation. |
FEMAP |
|
|
Load time history is exciting the Flexible-Body –System is given |
Modal Superposition: Modal stresses and coordinates are calculated and superpositioned similar to the static solution. |
RecurDyn / FEMAP |
|
Transient Analysis: Importing the stress tensor-time function from the FEM/MKS calculation. |
FEMAP |
||
|
Power spectral density |
Random Fatigue: |
Calculation possible but extensive preparatory work necessary by the user. |
*** Interface shipped on winLIFE Installation-CD
** Macros and examples supported from winLIFE customers
* winLIFE-customers use this software together with winLIFE successfully and prepared the interface themselves.
No support given by Steinbeis
Super position of standard FE loading conditions: rigid body under the influence of time-variable loads
If a rigid body is subjected to one or more loadings (force, moment), then it is possible to calculate the stresses and strains occurring locally by a combination of the (measured) load-time-functions with the statically determined standard loading conditions.
The stress tensors obtained from the standard loading conditions are scaled with the measured load-time-functions and super positioned for each time step. The result is a stress tensor-time function which is the basis for the damage accumulation calculation. This procedure can be used if the deformations in the body are relatively small compared to its measurements.
For the example (see diagram) you will need:
The path of the forces as a function of time (time series): F1(t),F2(t),F3(t)
The results of the related standard FE loading conditions. In each case a force FFE1, FFE2, FFE3 acts with the same line of action and point of application as the corresponding force. The results of the FE-calculation are the stress tensors in each (surface) node of interest for each loading condition.

Non-linear, Transient Analysis: Variable Component Geometry and Time-Variable and/or Direction-Variable Loadings
If the body changes its geometry considerably or if the directions of the acting forces change or if inertial forces occur, then the super positioning method described above is no longer a suitable calculation method. For example, if the shovel of a digger (see diagram) can be moved such that the three angles, alpha, beta und gamma are time-variable. The external loading also changes due to the load being transported.
In this case it is possible to calculate the digger behaviour using a MKS/FEM simulation. The forces and stresses at each point of interest can be calculated. Even the stress tensor which completely describes the stress state can be obtained. If you export the stress tensor for each time step t of the node of interest k, then a fatigue life calculation based on this can be carried out by winLIFE.
In this way you can examine other geometrically non-linear variable components and also oscillation conditions.

Parts under the influence of a dynamic, multiaxial load
It is particularly problematic to calculate the fatigue life for parts where a dynamic load results in considerable changes in the principal stress direction. This is because it is much more complicated to find out the load spectrum and to calculate here, compared to when the direction of the principal stress remains the same.
This problem can be found in many areas of technology, however, such as in a bodywork structure, axle components, crankshafts, rotary blades for wind power stations etc.

The figure above shows the example of steering under dynamic loading. It is influenced by horizontal and vertical force groups F1 und F2 . Because the forces are not proportional, a large change in the direction of the principal stress occurs. This is referred to as a multiaxial Problem.

For the calculation, it is only necessary to take into account the stresses on the surface because a tear usually begins on the surface. The stresses on the surface form an even stress condition. This makes the analysis considerably easier.
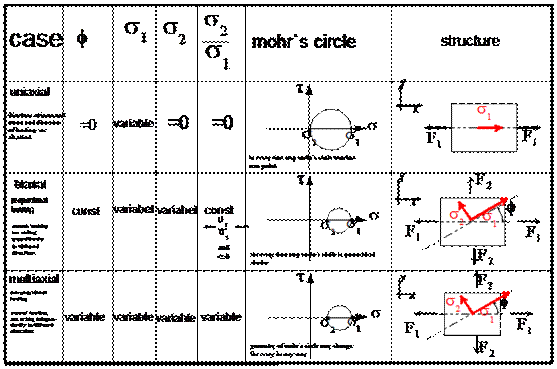
If the angle f or the ratio of the two principal stresses s2/s1 is variable over time, it means that we are dealing with a multiaxial case. Mohr’s stress circle can also be used to decide.
Because it is possible to calculate a multiaxial problem in a simple way without disadvantages if the change of stress direction is only small, the grade of multiaxiality must be determined at the start. For this purpose WinLIFE shows the angle f and the principal stress ratio s2/s1 for characteristic time steps presented by a point ().The location of the points helps to identify whether a multiaxial problem really exists or if a simplified calculation can be done by assuming that the case is biaxial.

Damage Parameter
Since the stress situation in the cutting plane consists of normal and shear stresses, these must be used to ascertain a damage equivalent size. The following equivalent stress hypotheses or damage parameters are possible:
- Normal stress - , shear stress and modified von Mises criterion,
- Findley
- Smith Watson Topper, P. Bergmann, Socie and Fatemi Socie,
Fatigue Life Calculation Depending on the Direction / Welded Joints
Particularly in the field of wind energy and ship building, structure stress concepts are common since very large components can hardly be calculated in any other way. In winLIFE several variations of structure stress concepts have now been included. You will need an entry file with the stress tensors extrapolated on the weld and the normal unit vectors.

How a fatigue life calculation is carried out
Using static FEA and superimpose according to (measured) load time histories
The calculation is carried out in the following steps as can also be seen in a simplified manner.
- Firstly, a FE loading condition must be calculated for each effective load. This must be done with a “unit load”.
- A material S-N curve must be defined in the same way as a stress S-N curve for a uniaxial case. In the case of Local Strain Approach an e-N-curve must be created.
- The time needed for the calculation can be considerably reduced if critical nodes are pre-selected. This selection can either be made by the user entering node numbers, or winLIFE can perform an automatic analysis to find the nodes that are most likely to be the critical ones.
- If a hysteresis is carried out and if you only take into consideration the reversals in common, then the load-time function can be reduced to the events relevant to the damage. This considerably reduces the time needed for the calculation.
- The stress tensor for each selected node and each time step is calculated based on the unit load cases and the load-time functions.
- Then, according to the critical cutting plane method, the shear stress and the normal stress is calculated for each node and time step for every plane. With this data, an equivalent stress or a damage parameter can be calculated. There are several hypothesis and damage parameters available, which the user has to select.
- The equivalent stress available for each node, time step and cutting plane is classed according to the rainflow method and a damage calculation is carried out. The plane with the greatest damage is the critical one. This result is taken as the damage for the node.

Modale Superposition
You can analyse properly dynamically loaded components by static superposition as described before only if the frequency of the excitation is less than 1/3 ot the first natural frequency of the system. If the condition is not met you need to decompose the signal in single shares for each natural frequency (modal coordinates). Furthermore you need to calculate the stress tensor for each natural fequency.
To performe the modal superposition you have to calculate two charateristic quantities:
- The natural frequencies and the related stress tensor
- The modal coordinates. These represent the share of the signal which excites the structure in the related frequency
This procedure is formally identical to the static superposition.
Using Strain gauges
When strain rosettes are used and the strain is measured, a fatigue calculation based on this data can be carried out. The data can be read directly and a flexible read-in tool is available (see next figure).
A fatigue prediction can be done for that point, where the measurement has been done.

How to reduce the calculation time
The extensive possibilities for interactively processing the load-time function are also available in the multiaxial module. It is therefore possible to process the load-time function interactively.
Analysis of the results
In a multiaxial case it is possible to analyse the results in the following ways:
- Mohr’s circle showing the critical cutting planes for each node and all considered time steps. The arising stress conditions can then be seen (diagram 6).
- largest principal stress vector for each node and all considered time steps
In addition there are numerous possibilities of showing the sum of damage with the FEA program post-processor.

The accuracy of the results for multiaxial problems will generally not be as good as those for uniaxial or biaxial problems. For this reason a conventional calculation should be carried out whenever possible in addition to the multiaxial calculation.
Reliable information can be ascertained regarding the critical places where a tear can be expected. Combining test results and the Relative Miner’s Law, it is also possible to make helpful forecasts regarding the quantity.
Partial load analysis
If several loads are acting on a component it is often interesting to know what influence the individual loads have on the damage sum. This can be ascertained with the partial load analysis.
We will now examine the following three alternatives. (To distinguish the alternatives, we use symbols recognisable from the set theory.)
- ∃ (= it only exists once) Only one of the existing loads is taken into account. The others are all set at Zero.
- - ∃ (=it does not exist exactly once) one of the acting loads is set at = 0 while all other loads remain unchanged.
- ∀∃ (as required) the user can select combinations as required.
For each existing load-time-function a column L1, L2, .. is created for the multiplicator. If this =1, then the load-time-function is used unchanged. If it is =0 the corresponding load-time-function will be set at =0.
The index column relates to the matrix line number.

Rotating Loadings / Load File Split
The calculation of rotating components is possible with a static superposition of scaled unit load cases. A rotation is observed in several equidistant splayed windows and the load-time function is broken up into individual load-time functions which only correspond to the value when within the splayed window. Outside the splayed window, they are equal to Zero.
Under the menu item Extras /Tools / Split Load an input mask opens. The contents of the file are shown in the window.
If there are any commentary lines, these will have to be skipped over. Enter the number of commentary lines in the designated box. In the example here there are no commentary lines (=0).
